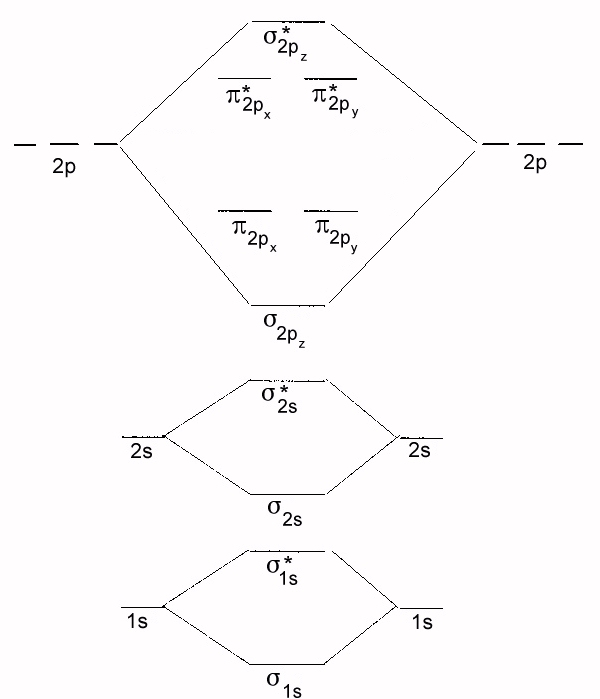
ANSWERS TO STUDY SHEET FOR CHEM 101 TEST 3 (DELANEY)



    1. FN2+, 3, dia

    2. F2, 1, dia

    3. C2, 2, para

    4. BBe, 0.5, para

    5. O2-, 1.5, para

    6. N2, 3, dia



    7. BF2-, 2, para

    8. CN-, 3, dia

    9. NO, 2.5, para

    10. CN-, 3, dia

  2. For each of the compounds below, draw the Lewis structure; then apply VSEPR theory to predict the molecular structure; name the molecular structure type; tell which hybrid orbitals would be used and final ly, draw the stucture.

    1. PBr3, tripodal, sp3



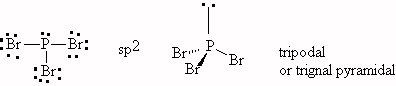
    2. CCl4, tetrahedral, sp3



    3. NH3, tripodal, sp3



    4. BF3, trigonal planar, sp2



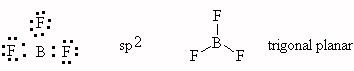
    5. PF5, trigonal bipyramid, sp3d



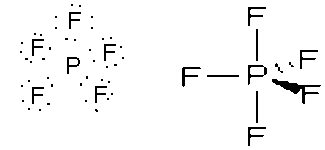
    6. SF4, wedge, sp3d



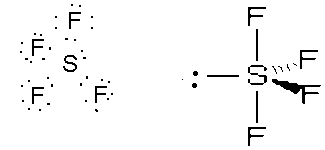
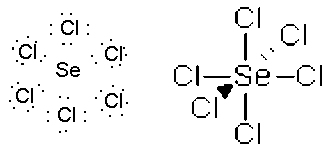
    7. SeCl6, octahedral, sp3d2



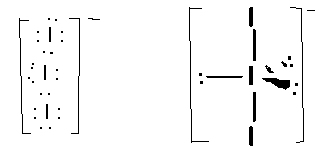
    8. I3-, linear, sp3d



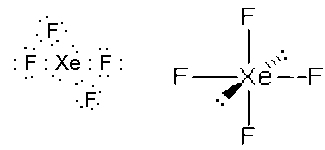
    9. XeF4, square planar, sp3d2



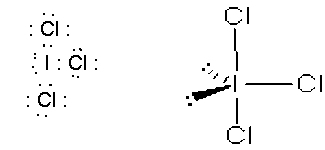
    10. ICl3, t-shaped, sp3d



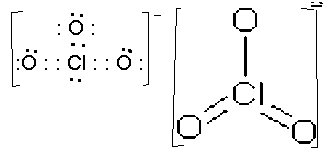
    11. ClO3-, trigonal planar, sp2 plus d orbital interactions in p bonds. Only one of three possible resonance structures is shown.




  3. Properly name the following compounds.

    1. MnSO4 manganese (II)sulfate

    2. AlPO4 alluminum phosphate

    3. P2O3 diphosphorus trioxide

    4. K3PO4 potassium phosphate

    5. KClO3 potassium chlorate

    6. Sc2S3 Scandium (III) sulfide

    7. N2O5 dinitrogen pentoxide

    8. Ca(NO3)2 calcium nitrate

    9. CoNO3 cobalt (I) nitrate

    10. FeSO4 iron (II) sulfate

  4. VSEPR theory stand for Valence Shell Electron Pair Repulsion theory. It considers each pair of electrons around a central atom as a -2 point charge. It predicts structure by considering these electron point charges as mobile when placed upon a shell around the central atom. Where the point charges end up due to the electrostatic repulsion of the minus 2 point charges for each other predicts the structure of the molecule.

  5. It turns out that linear combinations of solutions (weighted averages) to the Schoedinger equation are also solutions. A solution to the Schroedinger equation is actually an orbital. So averaging orbitals actually gives you new solutions. I just so happens that the geometries agree exactly with those predicted by VSEPR. AX2 molecules use sp hybrid orbitals; AX3 and AX2E molecules use sp2 hybrid orbitals; AX4, AX3E and AX2E2 molecules use sp3 hybrid orbitals; AX5, AX4E, AX3E2, and AX2E3 molecules use sp3d hybrid orbitals; and AX6, AX5E, and AX4E2 molecules use sp3d2 hybrid orbitals.

  6. The molecular orbitals are formed by averaging atomic orbitals on different atoms positions. It s similar to hybridizing atomic orbitals in valence bond theory, only the orbitals are on different atoms.

  7. A general rule for all orbitals is the more nodes, the higher in energy the orbital.



    1. Define:

      1. bonding orbital-a molecular orbital which puts electron density between or above or below the potential bond between two atoms. It is designated by either no superscript or a superscript

      2. anti-bonding orbital-a molecular orbital that has no electron density between or above or below the axis of a potential bond between two atoms. It is designated with a superscript *

      3. molarity: Moles of solute per liter of solution, mol/L, abbreviated M.

      4. percent by mass: {(mass a)/(mass A + mass B +...)} x 100 = {(mass A)/(Total mass)} x 100

      5. normality: (equivalents of H+, OH- or e-)/L . N = M x eq/mol, M = N/(eq/mol)

      6. Arrhenius acid: A material that provides H+ when dissolved in water.

      7. Arrhenius base: A material which provides OH- when dissolved in water.

      8. Bronsted Lowry acid: A material which provides H+.

      9. Bronsted-Lowry base: A material which accepts H+.

      10. oxidation is the lass of electrons.

      11. reduction is the gain of electrons.

      12. neutralization reaction: A reaction between and acid and a base yielding a salt and water.

      13. precipitation reaction: A reaction in which a solid fall out of solution.

      14. gas-evolving reaction: A reaction in which a gas bubbles out of solution, leaving the solution.

      15. addition or synthesis reaction: A reaction in which two or more reactants combine to make one product.

      16. decomposition reaction: A reaction in which one reactant yields two or more products.

      17. single displacement reaction: a reaction in which one element displaces another in a compound.

      18. double displacement or metathesis reaction: A reaction in which all the ions swap partners.

    2. Predict the products for the reaction between the paired elements below and write a balanced equation:

      Procedure: First predict the products using single atoms of the elements, and then write a balanced equation using the elemental forms of the elements for the reactants

      Elemental forms: Al, Li, Mg, O2, N2, F2, P4 and S8<

      1. O and Li; ion forms Li+ and O2- product is Li2O

        balanced equation: 4 Li + O2 6 Li2O

      2. P and S ;S is more electronegative than P, so P can formally Alose@ all five valence electrons, formal oxidation states would be P5+ and S2- so the product would be P2S5

        balanced equation: 4 P4 + 5 S8 6 8 P2S5

      3. S and F; F is more electronegative than S, so S can formally Alose@ all six valence electrons, formal oxidation state would be S6+ and F- so the product would be SF6

        balanced equation: S8 + 24 F2 6 8 SF6

      4. Al and F ionic compound, ion forms are Al3+ and F- so the product is AlF3

        balanced equation: 2 Al + 3 F2 6 2 AlF3

      5. Mg and N ionic compound, ion forms are Mg2+ and N3- so the product is Mg3N2

        balanced equation: 3 Mg + N2 6 Mg3N2





    1. 2 Ca + O2------> 2 CaO addition

    2. CaSO4 + 4 C -----> CaS + 4 CO

    3. C3H8 + 5 O2 -----> 3 CO2 + 4 H2O special=combustion

    4. P2O5 + 3 H2O -----> 2 H3PO4 addition

    5. Na2O + H2O -----> 2 NaOH addition

    6. 2 C4H10 + 13 O2 -----> 8 CO2 + 10 H2O special=combustion

    7. 3 Mg(OH)2 + 2 H3PO4 -----> Mg3(PO4)2 + 6 H2O double displacement, special=neutralization

    8. 2 HCl + Ba(OH)2 -----> BaCl2 + 2 H2O double displacement, special=neutralization

    9. 2 HgO -----> 2 Hg + O2 decomposition

    10. 2 AgNO3 + BaCl2 -----> 2 AgCl9 + Ba(NO3)2 double displacement, special=precipitation

    11. 2 H2O2 -----> 2 H2O + O2 decomposition

    12. C6H12O6 -----> 6 C + 6 H2O decomposition

    13. HC2H3O2 + NaOH ------> NaC2H3O2(aq) + H2O double displacement, special=neutralization



    1. no ionic compounds soluble in water

    2. CaSO4 is somewhat soluble in water, weak electrolyte

    3. all gaseous

    4. H3PO4 soluble in water, weak electrolyte

    5. NaOH soluble in water, strong electrolyte

    6. gaseous reaction

    7. H3PO4 soluble in water( weak electrolyte), Mg(OH)2 and Mg3(PO4)2 insoluble in water

    8. HCl,Ba(OH)2 and BaCl2 soluble in water, all electrolytes

    9. no ionic compounds soluble in water present

    10. AgNO3,BaCl2, and Ba(NO3)2 soluble in water, AgCl insoluble in water

    11. H2O2, solbule in water, non-electrolyte solution

    12. C6H12O6, glucose a covalent compund that is soluble in water due to the polar bonds it contains, non-electrolyte solution

    13. HC2H3O2,NaOH and NaC2H3O2, soluble in water, HC2H3O2 is weak electrolyte, NaOH and NaC2H3O2 are strong electrolytes



    1. true molecular

    2. true molecular

    3. true molecular

    4. true molecular

    5. true molecular

    6. true molecular

    7. molecular: 3 Mg(OH)2(s) + 2 H3PO4(aq) -----> Mg3(PO4)2(s) + 6 H2O

      total ionic: 3 Mg(OH)2(s) + 6 H+(aq) + 2 PO43-(aq) -----> Mg3(PO4)2(s) + 6 H2O

      net ionic: 3 Mg(OH)2(s) + 6 H+(aq) + 2 PO43-(aq) -----> Mg3(PO4)2(s) + 6 H2O

    8. molecular: 2 HCl(aq) + Ba(OH)2(aq) -----> BaCl2(aq) + 2 H2O

      tot.ion.: 2 H+(aq) + 2 Cl-(aq) + Ba2+(aq) + 2 OH-(aq) -----> Ba2+(aq) + 2 Cl-(aq) + 2 H2O

       net ionic: H+(aq) + OH-(aq) -----> H2O

    9. true molecular

    10. molecular: 2 AgNO3(aq) + BaCl2(aq) -----> 2 AgCl(s) + Ba(NO3)(aq)

      tot. ion.: 2 Ag+(aq) + 2 NO3-(aq) + Ba2+(aq) + 2 Cl-(aq) -----> 2 AgCl(s) + Ba2+(aq) + 2 NO3-(aq)

      net ionic: Ag+(aq) + Cl-(aq) -----> AgCl(s)

    11. true molecular

    12. true molecular

    13. molecular: HC2H3O2(aq) + NaOH(aq) ------> NaC2H3O2(aq) + H2O

      tot. ion.: H+(aq) + C2H3O2-(aq) + Na+(aq) + OH-(aq) ------> Na+(aq) + C2H3O2(-aq) + H2O

      net ionic: H+(aq) + OH-(aq) ------> H2O

  14. Define subscript, coefficient, yields arrow, (g), (s), (l), (aq), D,

    subscript-number in formula indicating atom ratio

    coefficient-number in front of a formula indicating ratio of moles or molecules to each other

    yeilds arrow-arrow going from reactants to products. Traditionally from left to right

    (g)-gaseous

    (s)-solid

    (l)-liquid

    (aq)-aqueous meaning dissolved in water

    8 - gas is evolved

    9 - a solid precipitates from solution

  15. A balanced chemical equation implies that 1) the mass on both sides of the yields arrow is the same, 2) the numbers of each type of atom on either side of the yields arrow is the same, and 3) the total charge on either side of the yields arrow is the same.

  16. Same as 3.

  17. Provide the formula weight and the weight percentage of each element in the compounds below. What is the empirical formula for each?

    1. H2SO3


      FW = 2(1.008)+32.06+3(16.00) = 82.08 g/mol

      %H = {[2(1.008)]/82.08}100 = 2.46%
      %S = {32.06/82.08}100 = 39.06%
      %O = {[3(16.00)]/82.08}100 = 58.48%
      EF = H2SO3

    2. HClO4

      FW = 1.008+35.45+4(16.00) = 100.46 g/mol
      %H = {1.008/100.46}100 = 1.00%
      %Cl = {35.45/100.46}100 = 35.29%
      %O = {[4(16.00)]/100.46}100 = 63.71%
      EF = HClO4

    3. Al(OH)3

      FW = 26.98+3(16.00)+3(1.008) = 78.00 g/mol
      %Al = {26.98/78.00}100 = 34.59%
      %O = {[3(16.00)]/78.00}100 = 61.54%
      %H = {[3(1.008)]/78.00}100 = 3.88%
      EF = Al(OH)3
    4. C6H12O6

      FW = 6(12.01)+12(1.008)+6(16.00) = 180.16 g/mol
      %C = {[6(12.01)/180.16}100 = 40.00%
      %H = {[12(1.008)]/180.16}100 = 6.71%
      %O = {[6(16.00)]/180.16}100 = 53.29%
      EF = CH2O

    5. NH4OH

      FW = 14.01+5(1.008)+16.00 = 35.05 g/mol
      %N = {14.01/35.05}100 = 39.97%
      %H = {[5(1.008)]/35.05}100 = 14.38%
      %O = {16.00/35.05}100 = 45.65%
      EF = NH4OH

    6. C5H5N

      FW = 5(12.01)+5(1.008)+14.01 = 79.10 g/mol
      %C = {[5(12.01)]/79.10}100 = 75.92%
      %H = {[5(1.008)]/79.10}100 = 6.37%
      %N = {14.01/79.10}100 = 17.71%
      EF = C5H5N

    7. C12H22O11

      FW = 12(12.01)+22(1.008)+11(16.00) = 342.30 g/mol
      %C = {[12(12.01)]/342.30}100 = 42.10%
      %H = {[22(1.008)]/342.30}100 = 6.48%
      %O = {[11(16.00)]/342.30}100 = 51.42%
      EF = C12H22O11

    8. K2Cr2O7

      FW = 2(39.10)+2(52.00)+7(16.00) = 294.20 g/mol
      %K = {[2(39.10)]/294.20}100 = 26.58%
      %Cr = {[2(52.00)]/294.20}100 = 35.35%
      %O = {[7(16.00)]/294.2}100 = 38.07%
      EF = K2Cr2O7

    9. CoFe2O4

      FW = 58.93+2(55.85)+4(16.00) = 234.63 g/mol
      %Co = {58.93/234.63}100 = 25.12%
      %Fe = {[2(55.85)]/234.63}100 = 47.61%
      %O = {[4(16.00)]/234.63}100 = 27.28%
      EF = CoFe2O4


  18. Find the empirical formulae of the compounds from the weight percentages given below. Find the empirical weight. Where appropriate, find the molecular formula.

    1. C - 92.3 %; H - 7.7 %; MW = ~78

      C92.3gH7.7g
      C92.3g/(12.01g/mol)H7.7g/(1.008g/mol)
      C7.685molH7.638mol
      C7.685mol/7.638molH7.638mol/7.638mol
      C1H1 = EF
      EW = 12.01 + 1.008 = 13.02 g/EF
      MW/EW = 78/13 = 6 therefore molecular formula is six times the empirical formula of C6H6.

    2. C - 92.3 %; H - 7.7%; MW = ~104

      Same as above, EW the same, MW=104
      104/13 = 8 therefore molecular formula is eight times the empirical formula, C8H8.

    3. C - 93.7 %; H - 6.3 %; MW = ~128

      C93.7 gH6.3 g
      C93.7g/(12.01 g/mol)H6.3g/(1.008 g/mol)
      C7.80molH6.25mol
      C7.80mol/6.25molH6.25mol/6.25mol
      C1.25H1 can't have fractions of an atom,& since 0.25=1/4 multiply through by 4 to give an empirical formula of C5H4
      EW = 5(12.01)+4(1.008) = 64.08 g/EF
      MW = 128; MW/EW = 128/64 = 2, therefore MF is twice EF or C10H8.

    4. Na - 32.4 %; H - 0.71%; P - 21.8 %; O - 45.1 %

      Na32.4gH0.71gP21.8gO45.1g
      Na32.4g/(22.99g/mol)H0.71g/(1.008g/mol)P21.8g/(30.97g/mol)O45.1g/(16.00g/mol)
      Na1.41molH0.704molP0.704molO2.82mol
      Na1.41mol/0.704molH0.704mol/0.704molP0.704mol/0.704molO2.82mol/0.704mol
      EF = Na2HPO4

    5. Co - 73.4 %; O - 26.6 %

      Co73.4gO26.6g
      Co73.4g/(58.93g/mol)O26.6g/(16.00g/mol)
      Co1.25molO1.66mol Co1.25mol/1.25molO1.66mol/1.25mol
      Co(1 atom)O(1.328 atom) (approximately 1.328 = 1 1/3 therefore multiply through by 3 to give an empirical formula of Co3O4.

    6. Fe - 36.8 %; S - 21.1 %; O - 42.1 %

      Fe36.8gS21.1gO42.1g Fe36.8g/(55.85g/mol)S21.1g/(32.06g/mol)O42.1g/(16.00g/mol)
      Fe0.659molS65.8molO2.63mol
      Fe0.659mol/0.658molS0.658mol/0.658molO2.63mol/0.658mol
      EF = FeSO4


  19. A compound is 38.70 % carbon, 9.75 % hydrogen and 51.55 % oxygen. What is the empirical formula of the compound?

    C38.70 gH9.75 gO51.55 g
    C38.70 g/(12.01 g/mol)H9.75 g/(1.008 g/mol)O51.55 g/(16.00 g/mol)
    C3.222 molH9.673 molO3.222 mol
    C3.222 mol/3.222 molH9.673 mol/3.222 molO3.222 mol/3.222 mol
    EF = C1H3O1 or CH3O

  20. What is the empirical weight of the compound in problem 16?

    EW = 12.01 + 3(1.008) + 16.00 = 31.04 g/EF

  21. If the approximate molecular weight of the compound in problem 16 is 86 + 5 g/mol , what is the molecular formula of the compound ?

    86/31.04 = 2.77
    minimum = 81/31.04 = 2.61
    maximum = 91/31.04 = 2.93
    May be C3H9O3, data does not fit exactly (Welcome to the real world!!!)

  22. Write the correct formula from the name

    1. ruthenium (III) nitrate, Ru(NO3)3

    2. beryllium iodide, BeI2

    3. cobalt (III) sulfate, Co2(SO4)3

    4. nitrous acid, HNO2

    5. sulfurous acid, H2SO3

    6. diarsenic trioxide, As2O3

    7. silver bromide, AgBr

    8. chloric acid, HClO3

    9. arsenous acid, H3AsO3

    10. phosphoric acid, H3PO4

  23. FW propane = 3(12.01)+8(1.008) = 44.09 g/mol

    moles propane = 25.0 g/(44.09 g/mol) = 0.567 mol

    FW dioxygen = 2(16.00) = 32.00 g/mol

    moles dioxygen = 25.0 g/(32.00 g/mol) = 0.781 mol

    moles of O2 required to react completely with o.567 mol of

    C3H8 = (5/1)(0.567 mol) = 2.835 mol of O2

    There are only 0.781 mol of O2 available, thus the limiting reactant is O2.

    Theoretical yield of CO2 = (3/5)(mol of limiting reactant)

    = (3/5)(0.781 mol) = 0.469 mol

    FW CO2 = 12.01 + 2(16.00) = 44.01 g/mol

    grams CO2 produced theoretically = (44.01 g/mol)(0.469 mol)

    = 20.6 g

  24. FW CoSO4 = 58.94+32.06+4(16.00) = 155.00 g/mol

    moles CoSO4 = 19.50 g/(155.00 g/mol) = 0.1258 mol

    FW NaOH = 22.99+16.00+1.008 = 40.00 g/mol

    moles NaOH = 8.50 g/(40.00 g/mol) = 0.2125 mol

    mol of NaOH required to react with 0.1258 mol of CoSO4 is equal to (2/1)(0.1258 mol) = 0.2516 mol of NaOH required

    There is only 0.2125 mol of NaOH, thus the NaOH will be all used up, and is the limiting reactant.

    Theoretical yield of both Co(OH)2 and Na2SO4 in moles:

    (2)(0.2125 mol) = 0.1063 mol

    FW Co(OH)2 = 58.94+2(16.00)+2(1.008) = 92.96 g/mol

    Actual yield in mol = 9.00g/(92.96 g/mol) = 0.0968 mol

    %Yield = [(0.0968 mol)/(0.1063 mol)]x100 = 91.1%

    OR

    FW Na2SO4 = 2(22.99)+32.06+4(16.00) = 142.04 g/mol

    Actual yield in mol = 13.75 g/(142.04 g/mol) = 0.0968 mol

    %Yield = [(0.0968 mol)/ (0.1063 mol)]x100 = 91.1%

  25. Fe(NO3)2 + Mg(OH)2 ------> Fe(OH)2 + Mg(NO3)2

    FW Fe(NO3)2 = 55.85+2(14.01)+6(16.00) = 179.87 g/mol

    moles Fe(NO3)2 = 20.21 g/(179.87 g/mol) = 0.1124 mol

    FW Mg(OH)2 = 24.31+2(16.00)+2(1.008) = 58.33 g/mol

    moles Mg(OH)2 = 5.93 g/(58.33 g/mol) = 0.1017 mol

    All ratios are 1:1. The lesser amount of moles is that of Mg(OH)2 so it is the limiting reactant. The amount of moles that theoretically can be produced for both Fe(OH)2 and Mg(NO3)2 is equal to (1/1)(0.1017 mol) = 0.1017 mol

    FW Fe(OH)2 = 55.85+2(16.00)+2(1.008) = 89.87 g/mol

    Actual yield of Fe(OH)2 = 8.82 g/(89.87g/mol) = 0.0981 mol

    %Yield = [0.0981 mol/(0.1017 mol)]x100 = 96.5%

    OR

    FW Mg(NO3)2 = 24.31+2(14.01)+6(16.00) = 148.33 g/mol

    actual yield Mg(NO3)2 =14.56/(148.33 g/mol)= 0.0982 mol

    %Yield = [0.0982/(0.1017 mol)]x100 = 96.6%



    1. FW Li2O2 = 2(6.940)+2(16.00)= 45.88 g/mol

      mol = 29.0 g/(45.88 g/mol) = 0.6321 mol

    2. FW U3O8 = 3(238.07)+8(16.00) = 842.21 g/mol

      mol = 576.01 g/(842.21 g/mol) = 0.68393 mol

    3. FW Fe(OH)3 = 55.85+3(16.00)+3(1.008) = 106.87 g/mol

      mol = 92.3 g/(106.87 g/mol) = 0.864 mol

    4. FW TiO2 = 47.90+2(16.00)= 79.90 g/mol

      6.17 g/(79.90 g/mol) = 0.772 mol

    5. FW Co2O3 = 58.94+3(16.00) = 107.02 g/mol

      11.9 g/(107.02 g/mol) = 0.111 mol



    1. FW H2S = 2(1.008)+32.06=34.08 g/mol

      g = (34.08 g/mol)(6.93 mol) = 236.17 g

    2. FW XeF4 = 131.30+4(19.00)= 207.30 g/mol

      (207.30 g/mol)(0.00655 mol)=1.358 g

    3. FW O2 = 2(16.00)=32.00 g/mol

      (32.00 g/mol)(6.98 mol) = 223.36 g

    4. FW U3O8 = 3(238.07)+8(16.00)= 842.21 g/mol

      (7.05 mol)(842.21 g/mol)= 5938 g

    5. FW ICl4 = 126.94+4(35.45)= 268.74 g/mol

      (0.1973 mol)(268.74 g/mol)=53.02 g

       

  28. Are the materials below acid anhydrides or basic anhydrides?

    1. Na2O basic anyhydride

    2. SO3 acidic anhydride

    3. P2O5 acidic anhydride

    4. MgO basic anhydride

    5. Cl2O7 acid anhydride

  29. What is the molarity of the solutions below?

    1. 3.998 g of LiOH dissolved in 15.00 mL of water

      FW LiOH = 6.94 + 16.00 + 1.008 = 23.95 g/mol
      moles LiOH = 3.998 g/23.95 g/mol = 0.1669 mol
      molarity = 0.1669 mol/0.01500 L = 11.27 M

    2. 59.99 g of LiCl dissolved in 135.88 mL of water

      FW LiCl = 6.94+35.45 = 42.39 g/mol
      moles LiCl = 59.99 g/42.39 g/mol = 1.415 mol
      molarity = 1.415 mol/0.13588 L = 10.41 M

    3. 20.00 g of Na3PO4 dissolved in 50.00 mL of water

      FW Na3PO4 = 3(22.99)+30.97+4(16.00) = 163.94 g/mol
      moles Na3PO4 = 20.00 g/163.94 g/mol = 0.1220 mol
      molarity = 0.1220 mol/0.05000 L = 2.440 M

    4. 55.00 g of H2SO4 dissolved in 35.00 mL of water

      HW H2SO4 = 2(1.008) + 32.06 + 4(16.00) = 98.08 g/mol
      moles H2SO4 = 55.00 g/98.08 g/mol = 0.5608 mol
      molarity = 0.5608 mol/0.05500 L = 10.20 M

    5. 100.00 g of C12H22O11 dissolved in 100.00 g of water

      FW C12H22O11 = 12(12.01) + 22(1.008) + 11(16.00) = 342.30 g/mol
      moles C12H22O11 = 100.00 g/342.30 g/mol = 0.2921 mol
      molarity = 0.2921 mol/0.10000 L = 2.921 L

  30. What is the molarity of an H2SO4 solution if a 20.00 mL sample of that solution is titrated with 26.97 mL of 1.225 M NaOH?

    NAVA = NBVB
    NA = NBVB/VA
    1.225 M NaOH (1 eq/mol) = 1.225 N NaOH
    NA = NBVB/VA = (1.225 N)(26.97 mL)/(20.00 mL) = 1.652 N H2SO4
    (1.652 N H2SO4)/(2 eq/mol) = 0.8260 M H2SO4

  31. What is the molarity of an LiOH solution if a 15.00 mL sample of the solution is titrated with 22.33 mL of 5.553 M HCl solution?

    NAVA = NBVB
    NB = NAVA/VB
    (5.553 M HCl)(1 eq/mol) = 5.553 N HCl
    NB = NAVA
    /VB = (5.553 )(22.33 mL)/(15.00 mL) = 8.267 N
    (8.267 N)/(1 eq/mol) = 8.267 M LiOH

  32. Are the compounds below soluble in water?

    1. Fe(C2H3O2)2 soluble

    2. PbSO4 insoluble

    3. NH4NO3 soluble

    4. AgCl insoluble

    5. MnSO4 soluble

    6. Fe(OH)2 insoluble

    7. KOH soluble

    8. Zn3(PO4)2 insoluble

    9. Na3PO4 soluble

    10. CaCO3 insoluble

  33. To what volume must 85.00 mL of 18.00 M H2SO4 be diltued to yield a solution that is 3.5565 M H2SO4?

    M1V1 = M2V2
    M1V1/M2 = V2 = (18.00 M)(85.00 mL)/(3.5565 M) = 430.2 mL

  34. What volume of 12.00 M HCl must you start with to successfully dilute it to 3.500 L of 2.450 M HCl?

    M1V1 = M2V2
    M2V2/M1 = V1 = (2.450 M)(3.500 L)/(12.00 M) = 0.7146 L or 714.6 mL